Aiken code
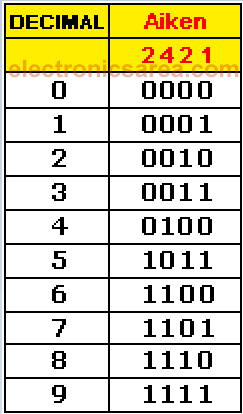
It is recommended to read the tutorial on the Binary number system before you start reading this tutorial. Aiken BCD code is similar to the natural BCD code, but with “weights” or “values” distributed differently. On the natural BCD, weights are: 8 – 4 – 2 – 1. On the Aiken code, the distribution is: 2 – 4 – 2 – 1.
The reason for this coding is to achieve symmetry between certain numbers. View the symmetry in the corresponding Aiken codes for decimal numbers: 4 and 5, 3 and 6, 2 and 7, 1 and 8, 0 and 9.
Decimal to Aiken Conversion table
Each number is the 9 complement of its symmetrical number, for all digits. The “1” becomes “0” and “0” becomes “1”. For example: 3 (0011) and 6 (1100). We must take into account the new “weights” on this code. The Aiken code is useful for operations of subtraction and division.
You may be interested on: The Gray Code, truth table and applications
Excess 3 Code
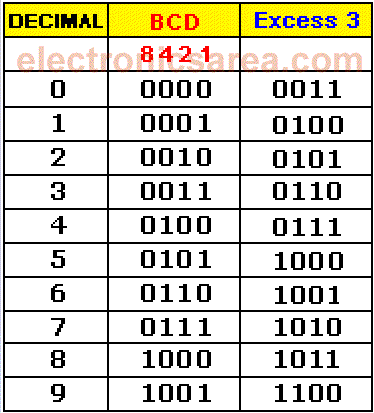
The Excess 3 Code is obtained by adding “3” to each combination of the natural BCD code.
The Excess 3 code is a code where the weighting does not exist (no “weights” as in the natural BCD and Aiken code).
Like the Aiken code, the Excess 3 code meets the same characteristic of symmetry. Each number is the 9 complement of its symmetrical number, for all digits.
Decimal to BCD to Excess 3 Conversion table
See the Excess 3 code symmetry, which corresponds to the decimal numbers: 4 and 5, 3 and 6, 2 and 7, 1 and 8, 0 and 9. It is a useful code in the operations of subtraction and division.
More Digital Tutorials
- What is the difference between Analog & Digital?
- What is a logic circuit?
- Digital logic levels (high, low, 1, 0)
- The truth table
- Boolean algebra
- Karnaugh Map (K-map)
- Binary number system
- Hexadecimal numbering system
- BCD code – binary coded decimal
- Gray code – Gray code table
- Aiken code – Excess 3 code
- AND gate
- NAND gate
- OR gate
- NOR gate
- NOT gate
- XOR gate
- How to build a NAND gate with transistors & diodes?
- OR & AND logic gates made with diodes
- The combinational circuit
- The sequential circuit
- JK Flip-Flop
- What is a binary decoder?