Gray code – Gray code Table

Jun 082023

What is Gray code?

We recommend reading the Binary Number System tutorial before you start reading this tutorial. The Gray code is named for Bell Labs researcher Frank Gray, who described it in 1947. This code is a special type of binary code that is unweighted (the digits that make up the code does not have an assigned weight).

The code main characteristic is that between one combination of digits (0, 1) and the next one, whether upstream or downstream, there is only a difference of one digit. So it is also called Progressive Code. This progression also occurs between the last and the first combination. That is why it is also called Cyclic code. (see the table)

Binary Code to Gray Code conversion method

To convert Binary into Gray, use the following method:

We add the binary number to another like it. The second number need to be moved one digit to the right. See the image.
We do a binary addition digit by digit, and we discard the carry.
We remove the last digit on the right side of the result on step 2 (we remove the zero, which is in red color). The resulting code is the GRAY code.

Gray code to Binary Conversion method

To convert a GRAY to a Binary, we use the following method:

The first digit of the Gray code will be the same in the binary number.
a) If the second digit is “0”, the second digit of the binary number is equal to the first digit.
b) If the second digit is “1”, the second digit of the binary number is the inverse of the first digit.
If the third digit is “0”, the third digit of the binary number equals the second digit of the binary number.
a) If the third digit is “1”, the third digit of the binary number is the inverse of the second binary number digit ….. And so on until finished.

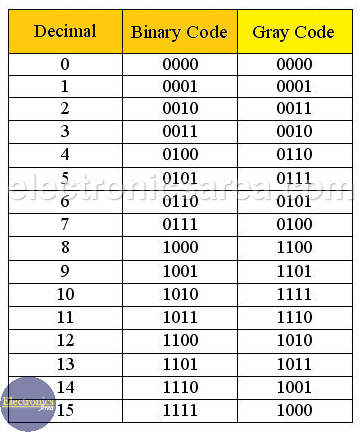
Decimal to Binary and Binary to Gray conversion (Gray code Table)

Gray code applications

Gray code can be used to simplify Boolean functions in Karnaugh maps. The advantage comes from the fact that this allows you to fill the K-map and make groupings in them. Thereby, it reduces the complexity and size of the original equation.

This code, is used mainly in position systems, either angular or linear. Its main applications are in industry and robotics. In Robotic, coded discs are used to give the position information that an axis have. This information is given in Gray code.

In communication systems, it is used to detect unexpected changes in data. If the bits in a number are summed, the sum of the next number should only change by one, with the sum alternating even and odd.

Binary and Gray code comparison

Analyzing the table above, we see that:

– When a binary number passes from:

0111 to 1000 (7 to 8 in decimal) or 1111 to 0000 (16 to 0 in decimal). All digits have changed.

– The same case but with the Gray code:

0100-1100 (7 to 8 in decimal) or 1000-0000 (16 to 0 in decimal). Only one digit has changed.

The characteristic of moving from one code to another, changing only one digit, ensures less chance of error.