What are resistors in series?
Series resistors are those that are connected in series and have the same current flowing or circulating through them.
What is the equivalent resistance of resistors in series?
The equivalent resistance value of resistors connected in series is equal to the sum of the values of all the resistors. Thus, Rts (equivalent resistance) = R1 + R2 + R3 + … + Rn, where “n” is the number of resistors in series.
Example 1:
What is the equivalent resistance of the following resistors in series: R1 = 10 ohms, R2 = 15 ohms, and R3 = 10 ohms?
Add the values of all the resistors we have: Rts = R1 + R2 + R3 = 10 + 15 + 10 = 35 ohms
What is the value of the current in the circuit?
The value of the current is the same in all the resistors (IR1 = IR2 = IR3 = ….. = IRn = IRts) and it is obtained with the formula
- IRs = V / (R1 + R2 + R3) in the case of 3 resistors in series.
- IRs = V / (R1 + R2 + R3 + …… + Rn), when there are “n” resistors in series.
Where V is the voltage across all the resistors in series.
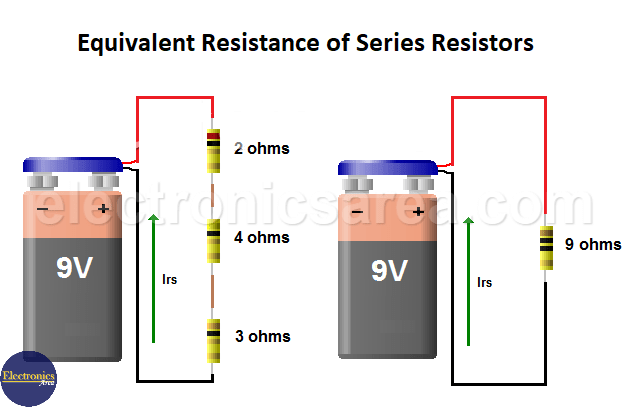
3 resistors in series and the equivalent resistor
With R1 = 2 ohms, R2 = 4 ohms, R3 = 3 ohms, V = 9 volts, and using Ohm’s law I = V/R, we get
Irs = V / Rts = 9 / (2+4+3) = 9/9 = 1 ampere.
What is the voltage across each resistor?
Once we have the value of the current flowing through the circuit, we can use Ohm’s law to determine the voltage drop across each of the resistors in the original circuit. V = I x R
- Across R1, the voltage drop is V1 = I x R1 = 1 ampere x 2 ohms = 2 volts.
- Across R2, the voltage drop is V2 = I x R2 = 1 ampere x 4 ohms = 4 volts.
- Across R3, the voltage drop is V3 = I x R3 = 1 amp x 3 ohms = 3 volts.
The sum of these 3 voltages is the supply voltage: V = V1 + V2 + V3 = 2V + 4V + 3V = 9 volts.
Example 2:
If we have 3 resistors in series, R1 = 220 ohms, R2 = 470 ohms, R3 = 330 ohms, and the applied voltage is 9 volts.
What is the equivalent resistance?
The equivalent resistance of 3 resistors in series is Rts = R1 + R2 + R3 = 220 + 470 + 330 = 1020 ohms.
What is the value of the current in the circuit?
Since the applied voltage is 9 volts, we can find the current in the series resistors using the formula
Irs = V / Rts = 9 / (220 + 470 + 330) = 9/1020 = 0.0088 Amps.
The current is the same in each resistor.
What is the voltage across each resistor?
Once we have the value of the current flowing through the circuit, we can use Ohm’s law to find the voltage drop across each of the resistors in the original circuit: V = I x R.
- Across R1, the voltage drop is V1 = I x R1 = 0.0088 amps x 220 ohms = 1.936 volts.
- Across R2, the voltage drop is V2 = I x R2 = 0.0088 amps x 470 ohms = 4.136 volts.
- The voltage drop across R3 is V3 = I x R3 = 0.0088 amps x 330 ohms = 2.93 volts.
The sum of these 3 voltages equals the supply voltage: V = V1 + V2 + V3 = 1.936 V + 4.136 V + 2.93 V = 9 volts.
Note: Although the calculations shown here were made using direct current, they also apply to alternating current, as long as the elements involved are resistors.
More resistor tutorials
- Resistors in Series – The Equivalent Resistance
- Resistors in parallel (Equivalent resistor value)
- Resistors in parallel (Equivalent resistor value)
- Series/Parallel Resistor Reduction
- What is Electrical Resistivity?
- Resistor Tolerance. What is it? – Color code
- Temperature effect on resistance
- What is Electrical Resistance? Obtaining a material’s resistance
- Wirewound Resistor
- LDR – Photoresistor