Home / Capacitors /
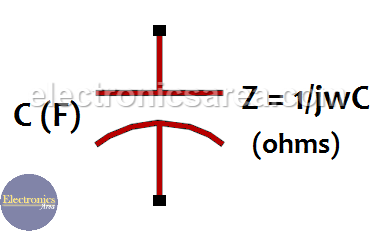
Impedance of a capacitor – Capacitive reactance
The Impedance of a capacitor (Capacitive reactance) is the measure of the opposition to a change of the electrical current in this component. It can be summarized, in a very general way, that a capacitor lets the high frequencies signals pass and blocks the low frequencies signals. (including 0 Hz signals)
The formula of the impedance of a capacitor (capacitive reactance) is: Z = 1/jCw
where:
- Z: is the impedance in ohms
- j: is the operator for imaginary numbers. (imaginary unit)
- C: is the capacitor value in Farads (C)
- w: is equal to 2.π.f, where the letter f represents the frequency of the signal applied to the capacitor. (frequency unit is Hertz).
The impedance – Capacitive reactance
Usually, capacitor are used in circuits with a frequency of signals different from zero (0 Hz).
We can see, from the impedance formula in a capacitor, that the impedance is inversely proportional to the frequency. This means that if the frequency is zero (0 Hz) the impedance is infinite.
Now, if the impedance is infinite, the voltage at the capacitor terminals is an open circuit and there is no current flow through the capacitor. Current = 0.
The impedance has a general formula: Z = V/I (RMS voltage / RMS current). This formula is similar to the Ohm’s law, which is applied to resistors, but in this case it is used for AC signals.
The “j” operator.
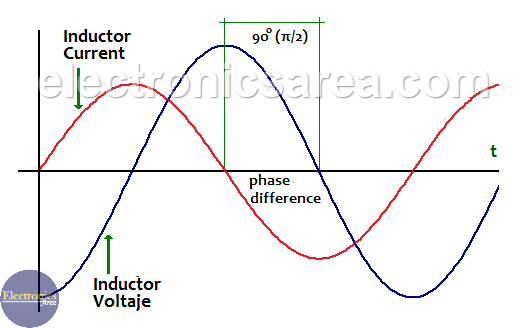
The reason why this operator is used in electronics is that there is a phase difference between the voltage and the current in a capacitor. This phase difference is 90° or π/2, and the current is ahead of the voltage by 90°. (90 degrees). The frequency of the voltage and current in a capacitor is the same.
Phase difference between voltage and current in a capacitor
The “j” operator is not used with the resistor because there is no phase difference between voltage and current. In other words, the voltage and current in a resistor are in phase.
w (angular frequency).
The value w depends directly on f (frequency) and is measured in radians/sec. (w = 2.π.f)
For example, for a frequency of 300 Hz, w = 2.π.f = 2 x (3.1416) x 300 = 1884.96 rad/sec.
How to calculate the Impedance of an inductor?
To calculate the impedance (capacitive reactance) of a capacitor, we use the formula Z = 1/wC.
Example 1:
Obtain the impedance of a 10uF capacitor at 300 Hz.
Z = 1/(2 x π x 300hz x 10uF) = 1/(2 x (3.1416) x 300 x 0.000010) = 53.05 ohms
Example 2:
Obtain the impedance of a 10uF capacitor at 50 Hz.
Z = 1/(2 x π x 50hz x 10uF) = 1/(2 x (3.1416) x 50 x 0.000010) = 318.31 ohms.
It can be seen from the two previous examples, where the value of the capacitor is the same (10uF), that the impedance is lower for higher frequencies. It can be summarized, in a very general way, that capacitors let pass high frequencies signals (there is low impedance) and blocks the low frequencies signals (there is high impedance).
Example 3:
Obtain the impedance of a 4700uF capacitor at 120 Hz.
Z = 1/(2 x π x 120hz x 4700uF) = 1/(2 x (3.1416) x 120 x 0.004700) = 0.2822 ohms.
Note: Xc = Capacitive reactance
