Home / Capacitors /
Capacitor Discharging Process
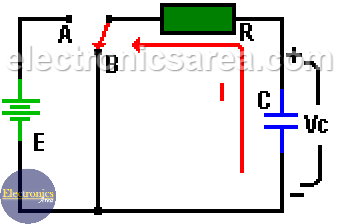
A fully charged capacitor in a series RC circuit is not immediately discharged after being disconnected from a direct current power source.
How do the capacitor discharge?
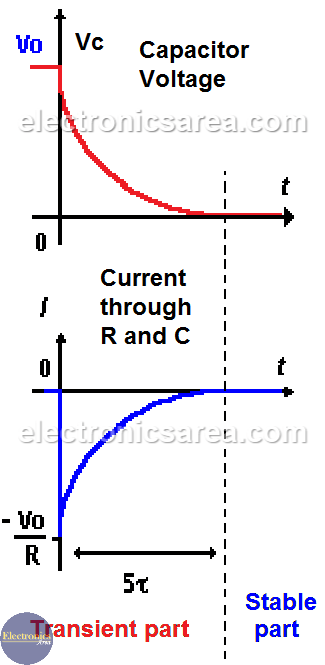
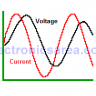
When the switch passes from the A position to the B position, the capacitor voltage Vc decreases from Vo (initial voltage on the capacitor) to 0 volts. (Look at the last image).
Current (I) has an initial maximum value of Vo/R amps and slowly decreases its value until it reaches 0 amps when the capacitor is completely discharged. (Look at the last image).
The current through the resistor (R) and the capacitor (C) is the same. Remember that in a series circuit the current is the same for all components.
The time (T) that takes the voltage in the capacitor (Vc) to go from the maximum voltage (E volts) until reaching 36.8% of the voltage of the power source is given by the formula: T = RC. Where the resistor value R is in ohms (Ω) , the capacitor C in millifarads (mF) and the result (time) is in milliseconds (mS).
After 5 x T (5 times T), the voltage has decreased to 0.7% of its initial value. The value of T is called: time constant.
The two images are divided into a transient part and a stable part. The values of Ic and Vc vary their values in the transient part, (approximately 5 times the time constant T), but not in the stable part.
- The value of Vc (capacitor voltage) for any instant is: Vc = Vo x e-t/T
- The value of I (current passing through R and C) at any instant is: I = -(Vo/R) x e-t/T
where: T = RC = Time constant
Transient and Stable Curves – Capacitor Discharging Process
Notes:
- Vo can be any voltage in the capacitor.
- If the capacitor was previously charged and has an initial voltage E, it is necessary to replace the Vo value with the E value in the previous formulas.