Capacitor Charging Process (RC circuit)

Capacitor Charging Process

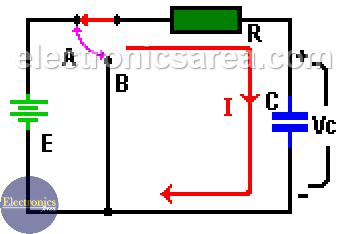
A capacitor is a device that, when connected to a DC power source, has an interesting behavior. See the diagram below.

When the “A” switch is closed, the current “I” suddenly increases to its maximum value (such in a short circuit) and has the value I = E/R amps. Then it gradually decreases until the current has a value of 0 “zero” amps, as shown in the diagram below.

On the capacitor charging process, the voltage across the capacitor does not change instantly when it rises from 0 to E volts. E is the value of the DC voltage source connected in series with R and C. (See the diagram).

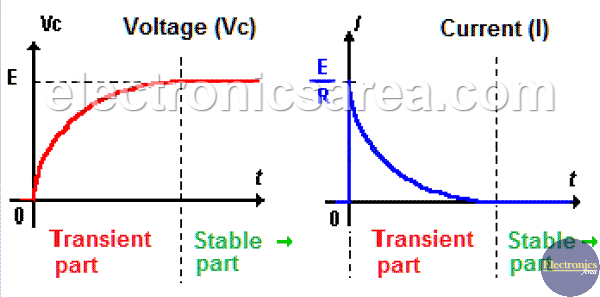
The time it takes the voltage on the capacitor (Vc) to go from 0 volts to 63.2% of the supply voltage (E) is specified by the formula: T = R x C, where:

• Resistor (R) is in ohms (Ω).
• Capacitor (C) is in millifarads (mF).
• Time (T) is in milliseconds. (mS).

After 5xT (5 times T) the voltage rises up to 99.3% of its final value. The value of T is called: “Time Constant”.  Analyzing the two charts below, we can see that they are divided into:

• A transient part where the values of Ic and Vc varies with time. (Approximately 5 times the time constant T).
• A stable part where values of Vc and IC are constant.

Vc, Ic and V_R values at any time, can be obtained using the following formulas:

• Vc = E + (Vo – E) x e^-t/T, where Vo is the initial voltage of the capacitor (in many cases this is 0 Volts).
• Ic = [(E – Vo) / R] x e^-t/(T/R), where Vo is the initial voltage of the capacitor (in many cases this is 0 Volts).
• V_R = E x e^-t/T

where: T = R x C.