Home / Capacitors /
Dielectric Constant / Relative Permittivity
The dielectric constant or Relative Permittivity is a dimensionless physical constant (Dielectric constant has no units) that describes how an electric field affects a material. The dielectric constant is the ratio of the permittivity of a substance to the permittivity of free space.
Capacity of a capacitor depends on the dielectric constant. It is known that the value of the capacity of a capacitor is given by the following formula: C = Q / V. Where:
- C: Capacitor capacity
- Q: capacitor charge
- V: Potential difference (voltage) between the capacitor plates
The capacitance of a capacitor can also be obtained differently by including the value of the dielectric constant.
How to obtain the Capacity, knowing the dielectric constant and its physical dimensions?
A capacitor is formed by two parallel plates. If there is a vacuum between these plates, the value of the capacity is: C = εo a / d. where:
- a = area of each plate in m2
- d = distance between plates in meters
- εo = dielectric constant in vacuum, whose value is: 8.85 x 10-12 farad / meter
If a dielectric is introduced between the plates, the capacitance will increase by a factor εr. So the capacity is:
C = εo εr a / d or C = ε a / d, where:
- ε = εo εr
- εr is the relative dielectric constant and depends on the physical properties of the medium used.
- ε is the absolute dielectric constant.
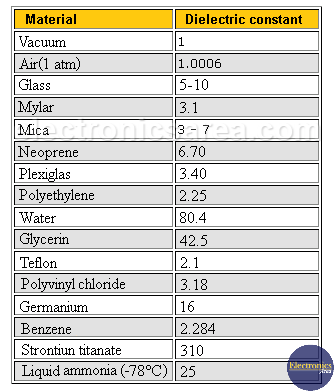
There is a great difference between values of the dielectric constants of different materials. Some important examples of dielectric constants are shown in the following table.
Table of dielectric constants
Table of dielectric constants (20 °C)
Example of capacity and charge calculation of parallel plate’s capacitor.
We have a parallel plates capacitor separated by vacuum. The plates are 1 mm apart and have an area of 2 x 10-6 meters. If the capacitor is connected to a voltage of 250 volts:
- What is the capacitance of the capacitor?
- What is the charge on each plate?
- What is the capacitance to be if it has a paper dielectric?
1. Capacitance:
Using the formula: C = εo εr a / d.
C = (8.85 x 10-12) (1) (2 x 10-6) / (1 x 10-3) = 1.77 x 10-14 Farads.
2. Charge on each plate:
Using the formula: C = Q / V, we obtain that Q = C x V.
Q = (1.77 x 10-14) x 250 = 4.425 x 10-12 Coulombs.
3. Capacitance with paper dielectric (εr = 2.5)
Using the formula: C = εo εr a / d
C = (8.85 x 10-12) (2.5) (2 x 10-6) / (1 x 10-3) = 4.425 x 10-14 Farads.
You can see the increase in capacitor capacity with a higher value dielectric.