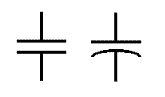What is a Capacitor?

Capacitors are devices made of two metal plates separated by an insulator or dielectric. A dielectric or an insulator is a material that prevents the flow of the electric current from one plate to the other.

Capacitors stores energy in the form of an electric field (it is clear when the capacitors work with direct current) and the capacitance is the amount of electric charges that it is capable to store.

Capacitor Symbols

“Capacitors” by Eric Schrader from San Francisco, CA, USA – 12739s. Licensed under CC BY-SA 2.0 via Wikimedia Commons.

Capacitance depends on the physical characteristics of the capacitor.

• If the area of the plates, that are face to face, is large, the capacitance increases.
• If the gap between plates increases, the capacitance decreases.
• The type of dielectric material between the plates also affects the capacitance.
• If you increase the applied voltage, the stored charge increases.

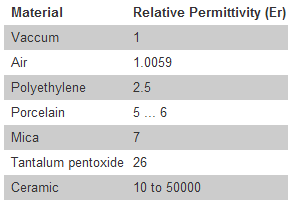
What is the dielectric material used for?

The dielectric material is used to increase the capacitance of the capacitor. Different materials are used as dielectric. These materials have different degrees of permittivity. (different capacities to create an electric field)

The greater the permittivity, the greater the capacitance. The capacitance is given by the formula: C = Er x A/d, where:

• C = capacitance
• Er = permittivity
• A = area between plates
• D = separation between the plates

The unit of measurement is the Farad. There are sub multiples such as: millifarad (mF), microcard (uF), nanofarad (nF) and picofarad (pF). The main electrical features of the capacitor are its capacitance and the maximum voltage between the plates (maximum voltage that can withstand the capacitor without damage).

Charge, Voltage and Capacitance Relationship

The electric current through a conductor is a flow of electric oriented charges. If a capacitor is connected to a direct current source, it receives an electrical charge. The value of the charge stored is obtained by multiplying the current delivered by the source and the time during which the source was connected to the capacitor.

Then: Q = I x t (charge = current x time), where:

• Q: charge in Coulombs
• I: current in amperes
• t: time in seconds

Experimentally, we can see that the charge stored in a capacitor is directly proportional to the voltage applied on its terminals. Then: Q = C x V (charge = capacitance x voltage), where:

• Q: charge in Coulombs
• C: capacitance in farads
• V: voltage in volts

Leveling the last equation with the first one, we obtain: Q = I x t = C x V. Clearing out: V = I x t / C.
If the values of C (capacitance) and the current remained constant, the voltage “V” will be proportional to the time. Then we can say that:

When a capacitor is charged with a constant current value,
the voltage on its terminals is proportional to the charging time.

Never connect a capacitor to a higher voltage than it can withstand
since it can explode.

More capacitor tutorials

• What is a Capacitor?
• Capacitors in series – Capacitors in parallel
• Capacitor in direct current (DC)
• Dielectric constant / Relative Permittivity
• Capacitor Charging Process
• Capacitor Discharging Process
• Capacitor in alternating current (AC)
• Impedance of a capacitor – Capacitive reactance of a capacitor
• Electrolytic capacitor