Resistors in Parallel – The equivalent resistance

Mar 222023
 

How to calculate resistor in series

To implement a circuit with resistors in series, you have to connect one resistor after the other one. (see the image). The equivalent resistor value of two or more resistors connected in series is equal to the addition of all resistor’s values.

In this case, the current flowing through all resistors in series is the same. Then:

RTS (series equivalent resistor value) = R1+R2+R3  (1)

The general formula to calculate the equivalent value of “n” resistors in series is:

RTS (series equivalent resistor value) = R1+R2+R3+……..+Rn-1+Rn  (2)

The electric current value in the equivalent circuit can be calculated using the Ohm’s law. (I = V/RTS). This current has the same value as the current on the original circuit.

Knowing the current that flows through the circuit, you can get the voltage across each resistor in the original circuit using the Ohm’s law.

  • Voltage on R1 is V1 = I x R1
  • Voltage on R2 is V2 = I x R2
  • Voltage on R3 is V3 = x I R3

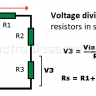
You can also find the voltage in a specific resistor using the voltage divider formula.

How to calculate Resistors in Series

For example:

If R1 = 10 ohms, R2 = 15 ohms and R3 = 10 ohms, then RTS = R1+R2+R3 = 10 + 15 + 10 = 35 ohms

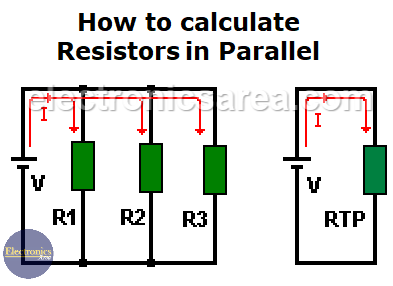
How to calculate resistors in parallel

On the series resistor circuit, the current has only one path to go from the positive to the negative battery terminal. In a parallel resistor circuit, the current supplied by the voltage source is divided in several paths.

If two or more resistors in parallel as shown in the picture, the current supplied by the voltage source is divided and the value of the current in each resistor depends on the resistor value. Using the Ohm’s law for each resistor:

I1 = V/R1, I2 = V/R2, I3 = V/R3

How to calculate Resistors in Parallel

The value of the equivalent resistance of the resistors in parallel is obtained with the formula: (for a 3 resistor circuit)

RTP (total parallel resistor value) = 1/(1/R1 + 1/R2 + 1/R3)    (3)

The general formula to calculate the equivalent value of “n” resistors in parallel is:

RTP (total parallel resistor value) = 1/(1/R1 + 1/R2 + 1/R3 + 1/Rn-1 + 1/Rn)    (4)

Showing the formula (3) in a slightly different way, we get: 1/RTP = 1/R1 + 1/R2 + 1/R3.    (5)

The total current delivered by the source is the addition of the individual currents in each resistor. The value of this current has the same value as the current in the equivalent resistor.

Then the current supplied by the voltage source is I = I1 + I2 + I3

For example:

If R1 = 10 ohms, R2 = 15 ohms and R3 = 10 ohms, then RTP = 1/(1/R1 + 1/R2 + 1/R3) = 1/(1/10 + 1/15 + 1/10) = 3.75 ohms

How to calculate resistors in parallel using conductance

If we use the conductance formula G = 1/R. (The conductance is the inverse of the resistance and its unit is Siemens), we can rewrite the above formula to obtain:

GTP = G1 + G2 + G3.    (6)

The equivalent conductance is the addition of conductance, so the equivalent conductance is the addition of the inverse resistors value.

GTP = 1/R1 + 1/R2 + 1/R3    (7)

As we may already know, the total conductance is the inverse of the total resistance GTP = 1/RTP. Clearing the last formula for RTP, we obtain:

RTP = 1/GTP    (8)

For example:

If R1 = 10 ohms, R2 = 15 ohms and R3 = 10 ohms, then G1 = 1/R1 = 0.1, G2 = 1/R2 = 0,0667 and R3 = 1/R1 = 0.1

The equivalent conductance is: GTP =  G1 + G2 + G3 = 0.1 + 0.0667 + 0.1 = 0.2667 Siemens

The equivalent resistance is: RTP = 1 / GTP = 1/0.2667 = 3.75 ohms.

Which is the equivalent resistor value of a set of resistors in parallel.

More resistor tutorials

You may also like:

 resistorss  Add comments

 Leave a Reply

(required)

(required)