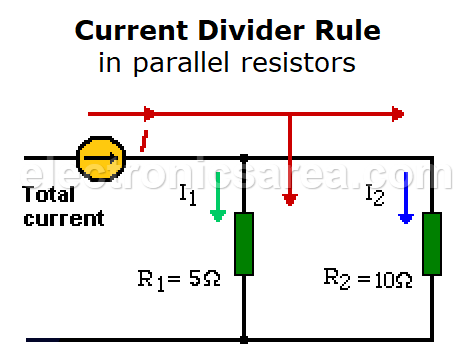
Current divider rule in parallel resistors
By using the current divider rule, we can find the current in each resistor connected in parallel. The electric current passing through a circuit of two resistors in parallel is divided in two.
Part of the current passes through the first resistor and the other part passes through the second one. The amount of current through a resistor depends on the value that the resistor has.
Finding the current using conductance
In order to know what is the current passing through each resistor, we can use the following formula: IR = CI/CR x IT. Where:
- IR = current in the resistor (the current we want to know)
- CI = conductance where the current IR flows.
- CR = equivalent conductance.
- IT = Total current.
Conductance C = 1/R
Total conductance of a parallel resistor is: CR = C1 + C2 + C3 +…. + CN
Current Divider Rule
Another method to find the current, a little longer, but easier to understand is:
- Get the total resistor value of all the parallel resistors. (RT)
- Using the total resistor value, the total current (IT) (we already know) and the Ohm’s Law, we can obtain the voltage on the terminals of the equivalent resistor.
- Again, using the Ohm’s Law, but this time for each resistor (Ri), we can obtain the current on each of them.
IR = (RT/Ri) IT = V/Ri
By using this method, we don’t need to the conductance.
Current divider calculation example
Looking at the diagram above. If the total current passing through the two parallel resistors (R1 and R2) is 6 amps, and if R1 = 5 ohms and R2 = 10 ohms, what is the current that circulates on each resistor?
- We get the equivalent circuit of the parallel resistors: RT = (R1xR2) / (R1+R2) = 5 x 10 /15 = 3.33 ohms
- The Ohm’s law gives the voltage applied to the two resistors.
V = I x RT = 6 amps x 3.33 ohms = 19.98 Volts (20 Volts). This voltage is the same for both resistors (remember that they are in parallel). - Using again the Ohm’s law, we can find the current in each resistor.
IR1 = V/R1 = 20/5 = 4 Amperes.
IR2 = V/R2 = 20/10 = 2 Amperes.
To check, we simply add the current that flows on each resistor to obtain the total current.
Total Current = IR1+IR2 = 4 amps + 2 amps = 6 amps.