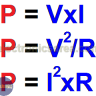Ohm’s Law Explanation
Ohm’s Law is named after the German physicist Georg Ohm (1789-1854). The Ohm’s law states that the voltage across a resistor is directly proportional to the current flowing through the resistor and directly proportional to the resistance of the circuit.
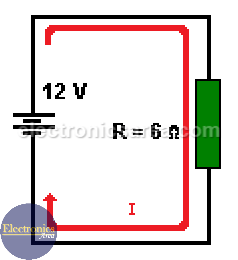
The formulas of Ohm’s law are: V = IR, I = V/R, and R = V/I. It can be easily understood if we analyze a circuit where there is a battery (12 volt power source) in series with a 6 ohm resistor.
To find the current: I = V/R
Therefore, the electric current flowing through the circuit (through the resistor) is I = 12 volts / 6 ohms = 2 amps.
To find the voltage: V = I x R
In the same way, we can solve the above equation for voltage, and we get V = I x R (another expression for Ohm’s law), so if we know the current and the value of the resistor, we can obtain the voltage across the terminals of the resistor as follows V = 2 amps x 6 ohms = 12 volts.
To find the resistance: R = V / I
As in the previous case, we can solve the equation for the resistance, and we get R = V / I. Then, if we know the voltage across the resistor and the electric current flowing through it, we get the resistance value: R = 12 volts / 2 amps = 6 ohms
It is interesting to note that the relationship between electric current and voltage across a resistor is always linear, and the slope of this line is directly related to the value of the resistor. Thus, the greater the value of the resistor, the greater the slope.
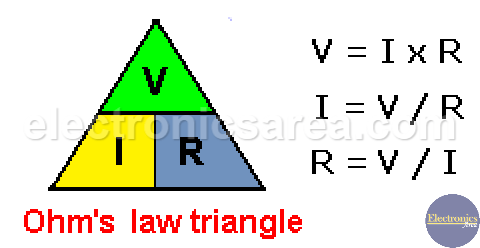
Ohm’s Law Triangle
The following triangle, which is very similar to the formulas discussed above, is used to memorize the three expressions of Ohm’s Law.
There are 3 cases:
- If there is a fixed resistance value, an increase in current means an increase in voltage.
- When the voltage is fixed, an increase in current is caused by a decrease in resistance.
- When the current is fixed, an increase in resistance causes an increase in voltage.
It is important to note that the data obtained can also be used to determine the power dissipated in a resistor. In this way, electrical power and Ohm’s law are related.
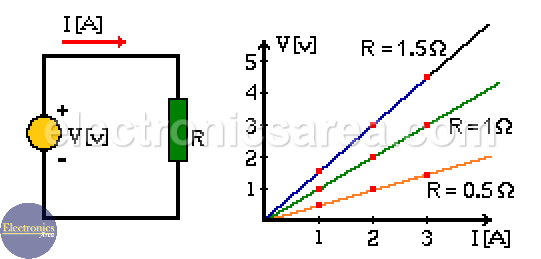
Ohm’s law for different resistor values
If we look at the picture, we can see three lines with different slopes, corresponding to three different resistor values.
From the picture above, we can see the current value for each resistor for a given voltage. We can also find the voltage value for each resistor for any given current.
Ohm’s law and electrical power
The Ohm’s Law triangle relates voltage, current and resistance in one equation. (Resistance = resistor value). A more complete expression of Ohm’s Law is the electrical power formula.
Using the well-known power formula: P = V x I, (power = voltage x current) and its variants: V = P/I and I = P/V, additional formulas are obtained.
These new equations allow us to obtain the values of power, voltage, current and resistance using only two of the four variables.
- Solving for P, we get: P = V2/R, P = I2 x R, P = V x I (watts)
- Solving for I, we get: I = V/R, I = P/V, I = (P/R)1/2 (amps)
- Solving for R, we get: R = V/I, R = V2/P, R = P/I2 (ohms)
- Solving for V, we get: V = (P x R)1/2, V = P/I, V = I x R (volts)
The following image shows a complete summary of the formulas, arranged for easier memorization.
Ohm’s Law and Electrical Power
Examples of Ohm’s Law and Electrical Power
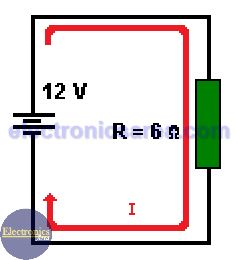
Problem: Find the power dissipated by a resistor R = 6 ohms connected to a battery of 12 volts.
1- If we solve the problem with the formula P = I2 x R
The electric current flowing through the circuit is I = 12 volts/6 ohms = 2 amps. We can find the heat dissipated by the resistor using the formula: P = I2 x R = 22x6 = 24 watts
2 – If we solve the problem using the formula: P = V x I
We can find the power on the resistor using the formula: P = V x I = 12 x 2 = 24 watts
We can find the heat dissipated by the resistor using the formula: P = V x I = 12 x 2 = 24 watts
3 – If we solve the problem using the formula: P= V2/R
In the same way, we can find the heat dissipated by the resistor using the formula: P = V2/R = 122 / 6 = 24 watts. This formula doesn’t require you to find the current flowing through the circuit.
Problem: What is the maximum current that can flow through a 5 watt resistor when connected to a 6 volt battery?
1- Solving the problem using the formula: I = P/V.
The electric current flowing through the resistor is: 5 watts/6 volts = 0.83 amps.
2- Solving the problem using the formula: I = V/R.
First, we find the resistance using the formula: R = V2/P = 62 / 5 = 7.2 ohms. Then we can find the current flowing through the resistor: I = V/R = 6 volts / 7.2 ohms = 0.83 amps.
3- Solving the problem using the formula: I = (P/R)1/2
First, we find the resistance using the formula: R = V2/P = 62 / 5 = 7.2 ohms. Then we can determine the current flowing through the resistor: I = (P/R)1/2 = (5 watts / 7.2 ohms)1/2 = 0.83 amps.
Note: The square root = ( )1/2.