What is Voltage divider?
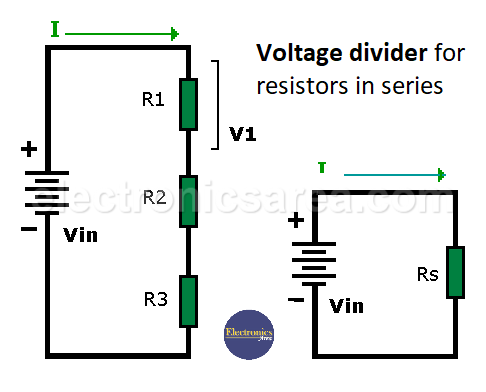
The voltage divider formula for series resistors, like the current divider formula for parallel resistors, is very important in circuit analysis. When two or more resistors are connected in series, the current flowing through them is equal. See the following diagram for a case of 3 resistors in series.
The equivalent resistance (Rs) of these series resistors is obtained by adding the values of all the resistors. Rs = R1 + R2 + R3 + … + Rn, where “n” is the number of resistors.
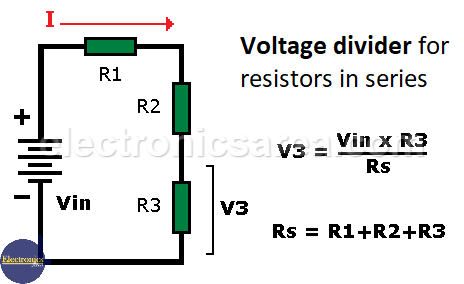
Once you have the equivalent resistance, you can use Ohm’s law to find the current: I = V/Rs. The figure below shows the original circuit and the equivalent circuit.
Since in series resistors the current is the same in all the resistors, the following formulas are obtained by using Ohm’s law for each of the resistors:
- I = Vin/Rs or
- I = V1/R1 or
- I = V2/R2 or
- I = V3/R3.
The voltage divider formula
Since the current I is the same in the previous equations, they can be equated. Then Vin/Rs = V1/R1. Assuming that the voltage to be known is V1, we solve for this value. V1 = Vin x R1 / Rs.
The voltages V2 and V3 are obtained in the same way, but with the corresponding resistor value. (For V2 change R1 to R2, for V3 change R1 to R3).
We can express the formula in words, then the voltage divider formula says:
Vout = (resistance across the output / total circuit resistance) x applied voltage (Vin).
We can also express the formula as Vout = (Rx / Rs) Vin, where “x” is the resistance number.
Voltage Divider Calculation Example
If the values of the resistors are R1 = 1 K, R2 = 2 K and R3 = 3 K, and the value of the source is Vin = 12 V, calculate the following:
– The voltage across resistor R3:
Vout = Vin x R3 / (R1+R2+R3)
Vout = 12V x 3K / (1K+2K+3K)
Vout = 12V x 3K / 6K
Vout = 12V/2 = 6V
Vout = V3 = voltage across resistor R3 = 6V
– The voltage across resistor R2:
Vout = Vin x R2 / (R1+R2+R3)
Vout = 12V x 2K / (1K+2K+3K)
Vout = 12V x 2K / 6K
Vout = 12V/3 = 4V
Vout = V2 = voltage across resistor R2 = 4V
– The voltage across resistor R1.
Vout = Vin x R1 / (R1+R2+R3)
Vout = 12V x 1K / (1K+2K+3K)
Vout = 12V x 1K / 6K =
Vout = 12V/6 = 2V
Vout = V1 = voltage across resistor R1 = 2 volts
To confirm that our calculations are correct, we add the voltages across the resistors and it should equal 12V, the value of the original source voltage “Vin”.
V1 + V2 + V3 = 2V + 4V + 6V = 12V.