Series/Parallel Resistor Reduction
To make a Series or a Parallel Resistor Reduction, it is only necessary to do some simplifications using formulas we already know. The situation is different when you have to simplify a circuit that is composed of combinations of resistors in series and resistors in parallel. In this case, a Series/Parallel Resistor Reduction is needed.
Series/Parallel resistor reduction procedure
To simplify a complex circuit and to obtain the equivalent resistance, we follow this procedure:
1 – You need to rearrange the circuit we want to simplify, to see clearly the component parts, and discover the parts that are already connected in series and parallel.
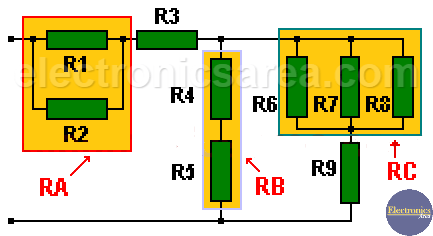
2 – We assign to each of these parts, a new name, such as RA, RB, RC, RD, etc. (look at the first image).
3 – We obtain the equivalent resistance of each part using the familiar formulas. (resistors in series and parallel resistances).
4 – We replace the parts in the original circuit with the values of the equivalent resistances (RA, RB, etc.) obtained in the previous step.
5 – We analyze the resulting circuit, and seek other possible combinations of resistance groups (parts) in series and parallel, which have been created.
6 – We repeat the process again from step 2 with different names for equivalent resistances to avoid confusion (e.g. RX, RY, RZ, etc.), until we obtain a single final equivalent resistance of the entire circuit.
Analyze the following image:
Series/Parallel Resistor Reduction
Resistors values are:
R1 = 120, R2 = 250, R3 = 68, R4 = 47, R5 = 68. (all in Ohms).
R6 = 5, R7 = 4, R8 = 2, R9 = 1.2. (all in Kilo ohms).
First reduction
- RA = R1 and R2 in parallel,
RA = R1//R2 = R1 x R2 / (R1 + R2) = 120 x 250 / (120 + 250) = 81 ohms. - RB = R4 and R5 in series,
RB = R4 + R5 = 47 + 68 = 115 ohms. - RC = R6, R7 and R8 in parallel,
RC = R6//R7//R8 = 1/( 1/R6 + 1/R7 + 1/R8) = 1/( 1/ 5K + 1/4K + 1/2K) = 1053 ohms.
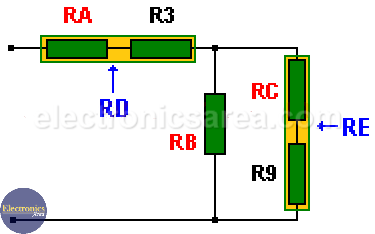
We replace the equivalent values, obtained in the previous steps, in the original circuit, and we get:
Series/Parallel Resistor Reduction Procedure
We simplify the circuit again, and we get new equivalent resistances. Then:
- RD = RA and R3 in series,
RD = RA + R3 = 81 + 68 = 149 ohms. - RE = RC and R9 in series,
RE = RC + R9 = 1053 + 1200 = 2253 ohms.
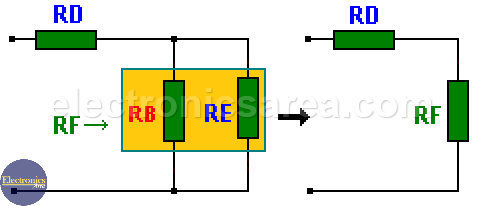
And replacing these latest data, the following circuit is obtained:
In the latter circuit it can be seen that RB and RE are in parallel, and we get a new RF equivalent resistance that is in series with RD:
RF = RB and RE in parallel,
RF = RB//RE = RB x RE / (RB + RE) = 115 x 2253 / (115 + 2253) = 109 Ohms.
RF is in series with RD. We add their values to obtain the final resistor value “Req”. That is the total equivalent resistance value of all the circuit.
Then:
Req = RF and RD in series,
Req = RF + RD = 109 + 149 = 258 ohms.
More resistor tutorials
- Resistors in Series – The Equivalent Resistance
- Resistors in parallel (Equivalent resistor value)
- Resistors in parallel (Equivalent resistor value)
- Series/Parallel Resistor Reduction
- What is Electrical Resistivity?
- Resistor Tolerance. What is it? – Color code
- Temperature effect on resistance
- What is Electrical Resistance? Obtaining a material’s resistance
- Wirewound Resistor
- LDR – Photoresistor