Home / Power Supplies /
Internal Resistance of a Voltage Source
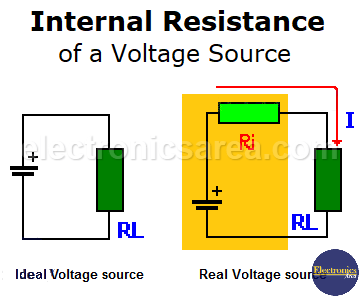
Voltage sources, whether batteries, generators, etc., are not ideal (perfect). A real voltage source is composed of an ideal voltage source in series with a resistance called internal resistance. This resistance does not really exist so that we can see it. It is a resistance deduced by the behavior of the real voltage sources.
See the diagrams of the ideal voltage source and the actual voltage source below.
- VI = Internal resistance voltage.
- VL = Load resistance voltage.
- RI = Internal resistance.
- RL = Load resistance.
Taking the following values: I = 4 Amperes, RI = 3 Ohms, RL = 5 Ohms.
- Voltage drop on the internal resistance: VI = I x RI = 4 amps x 3 ohms = 12 volts
- Voltage drop on the load resistor: VL = I x RL = 4 amps x 5 ohms = 20 volts
The total voltage drop will be: VI + VL = 12 V + 20 V = 32 Volts (equal to the voltage of the ideal source) (Kirchhoff voltage law).
It can be clearly seen that only 20 of the 32 volts are applied to the load (RL), the remaining voltage is lost in the internal resistance. Frequently, this voltage (VL = 20 volts) is called terminal voltage, because it is measured at the terminals of the voltage source.
How is internal resistance obtained?
To obtain the internal resistance in a voltage source, these steps must be followed:
- The voltage at the terminals of an uncharged voltage source is measured. The measured voltage will be VNL (voltage without load)
- A load is connected to the voltage source and the voltage is measured. The measured voltage will be VL (voltage with load)
- The current of the source with load is measured. The measured current will be I
Once these values are available, the following equation is applied: RI = (VNL-VL) / I (1)
For example:
If VNL = 12 volts, VL = 11.8 volts and I = 10 Amperes, then the internal resistance is RI = (12V – 11.8V) / 10A = 0.02 ohms.
From the last equation (1) we can get: VL = VNL – (I x RI), so…
If the electric current I grows to 25 amps (meaning that the load resistor have a smaller value), the load voltage is : VL = 20 volts – (25 amps x 0.02 ohms) = 11.5 volts.
We can conclude that, the more electric current the load (RL) demands, the lower the terminal voltage due to the greater voltage drop in the internal resistance (RI).
Power transfer between a voltage source and a load is at its most efficient when the resistance of the load matches the internal resistance of the voltage source.