BCD code: binary-coded decimal.

Mar 202023

BCD Code (Binary Coded Decimal)

To share digital information, binary and hexadecimal representations are commonly used. There are other methods of representing information, one of which is BCD (binary-coded decimal) code.

This code makes it easier to see the relationship between a decimal number and its binary counterpart. Decimal numbers are base 10. Binary numbers are base 2.

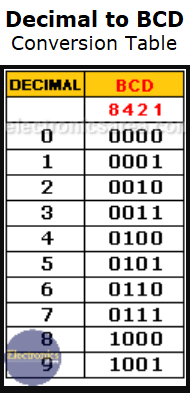
This code uses four binary digits to represent a decimal digit (0–9), as can be seen in the two examples that follow. However, when converting a BCD binary number back to its decimal form, there is no direct relationship between the two.

There are other codes, such as the Gray code, which involves a specific ordering of binary numbers so that two consecutive values differ by only one bit. This is used for position detectors where it is necessary to determine relative position.

Examples of converting decimal numbers to BCD code

Example 1: The direct conversion of the decimal number 85 to binary is: 85₁₀ = 1010101₂.

The representation of the same decimal number in BCD is demonstrated in the following image.

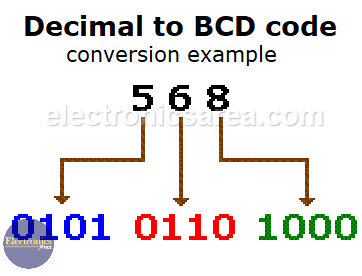
Example 2: Direct conversion of the decimal number 568 to binary:: 568₁₀ = 1000111000₂.

The representation of the same decimal number in BCD is demonstrated in the following image.

As the previous two examples show, the binary number representation does not resemble the final BCD representation.

How can the BCD code of each decimal number be obtained?

To obtain the BCD equivalent of each decimal digit, a ‘weight’ or ‘value’ is assigned to each digit according to its position.

This ‘weight’ or ‘value’ follows the following order: 8 – 4 – 2 – 1 (it is a weighted code). The last example shows that the number 5 is represented as follows: 0 1 0 1.

The first ‘0’ corresponds to 8.
The first ‘1’ corresponds to 4.
the second ‘0’ corresponds to 2.
and the second ‘1’ corresponds to 1.

From the above chart: 0x8 + 1×4 + 0x2 + 1×1 = 5.

The BCD code with the ‘weights’ or ‘values’ described above is called: Natural BCD code. This code counts in the same way as a normal binary number, from 0 to 9. However, numbers from 10 (1010) to 15 (1111) are not allowed, as there is no equivalent decimal number for these values.