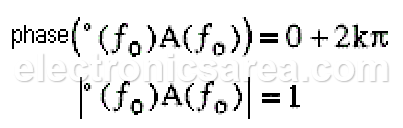Basic structure of the sinusoidal oscillator
The sinusoidal oscillator basic structure consists of an amplifier (A) and a selective frequency network (ß) connected in a positive feedback loop as shown in the block diagram below.
Although in an oscillator, there is no input signal, it is possible to obtain the loop gain of the amplifier (Af) which, due to the positive feedback, has the following formula:
Where A = A(ƒ) and ß = ß(ƒ) are dependent on the frequency ƒ. If there is a frequency ƒo that causes that ßA = 1, then the value of Af in the above equation is infinite. That is, at this frequency, with zero input, the output of the circuit is finite. This circuit is by definition an oscillator.
The condition for the circuit to provide sinusoidal oscillations at frequency ƒo is:
The Barkhausen criterion for oscillation sets these conditions: at frequency ƒo, the phase of the loop gain should be 0+2kp and magnitude of the loop gain should be 1. Expressed more formally, the Barkhausen criterion for oscillation requires that: