What is Impedance?
Impedance (Z) shows the opposition to the flow of direct or alternating current. Impedance is the vector addition of resistance and reactance.
The resistance is the opposition’s value to the flow of the electric current (whether direct current or alternating current). The reactance is the opposition’s value to the flow of the alternating current through a capacitor or inductor.
The opposition to the alternating current in a capacitor is called capacitive reactance, and the opposition to the alternating current in an inductor is called inductive reactance.
Impedance (Z) = Resistance (R) + Reactance (X)
When these elements (resistors, capacitors and inductors) are combined in the same circuit and an alternating current flows through them, the opposition of this set of elements to the flow of the alternating current is called Impedance.
The Impedance unit is Ohm, and it is equal to the phasor addition of a resistive value (resistance) and a reactive value due to a reactive components (inductors and capacitors): Z = R + jX
The “j” operator that goes before the X capital letter, tells us that X is an imaginary number. This is not a common addition, It is a phasor addition (sum of phasors).
Impedance phase shift
The inductor and capacitor cause an opposition to the flow of the alternating current (plus a phase difference), but they do not ideally cause any dissipation of power, as in the resistor (Joule’s Law).
There is a phase shift between the voltage and the current that flows through the capacitor and / or inductor. The voltage gets behind the current on the capacitor. The current gets behind the voltage on the inductor.
This phase shift, on inductor and capacitor, is opposites, and if they have the same magnitude they would be cancelled and the total impedance of the circuit would be equal to the value of the resistor. (see the formula above).
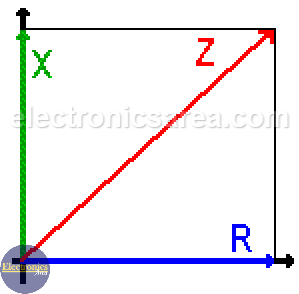
The formula Z = R + jX is represented by the picture above. You can see that:
- The reactance are on the y-axis (the imaginary axis) and they may go up or down, depending on wish influence is higher, the one of the capacitor or the one of the inductor.
- The resistance is always on the X-axis. (It is only on the positive side).
Fhase shift formula = φ = tan-1( (wL – 1/wC) / R ) = φ = tan-1( (XL – XC) / R )
Impedance formula
The value of the impedance (the diagonal line) is: Z = (R2 + X2)1/2.
Example of impedance calculation in an RLC series circuit
Calculate the impedance of a circuit RLC in series with R = 10 ohms, C = 470 uF, L = 2 henry and F = 1 Khz.
- Z = R + (XC + XL) = R + ( ( 1/jwC) + jwL ), w = 2πf
- w = (2)(3.1416)(1000) = 6283.2
- XC = 1/jwC = 1/j(6283.2)(4700 x 10-6) (Capacitive reactance)
- XL = wL = j(6283.2)(2) (Inductive reactance)
- Z = ( R2 + (XC + XL )2 )1/2 = 0.016 ohms
Impedance phase shift
φ = tan-1( (wL – 1/wC) / R ) = 51.41°
Note: The parentheses to 1/2 power is equal to a square root.