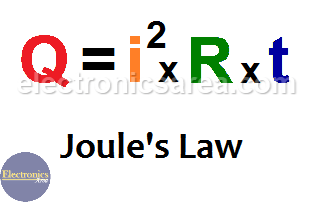What is Joule’s Law? The Joule effect

It is known as Joule effect to the phenomenon by which if in a wire circulates an electrical current, part of the energy is transformed into heat. The Joule’s Law is named after the British physicist James Prescott Joule.

Joule’s law shows the relationship that exists among

• The current that flows through a wire.
• The heat generated by the current that flows through a wire.
• The resistance of the wire and …
• The time the current passes through the wire.

Joule’s Law formula (amount of heat)

Joule’s law formula is: Q = I² . R . t, where:

• Q is the amount of heat, in Joules (J)
• I is the electric current that flows through the wire, in amperes (A)
• R is the value of the electrical resistance of the wire, in ohms (R)
• t is the amount of time that current passes through the wire, in seconds (s).

Joule’s law can be established as the amount of heat (Q) generated in a wire with resistance (R), when a current (I) passes through it for a period of time (t).

This heat is directly proportional to:

• The square of the current.
• The resistance of wire.
• The time the current flows through the wire.

What are the heating effects caused by electric current?

When a current flows in a wire, thermal energy is generated in it. The heating effects caused by electric current depend on three factors:

• The resistance of the wire. Higher resistance produces more heat.
• The time that current flows through the wire. The greater the time, the greater the heat generated.
• The greater the current, the more heat generation.

Some applications of Joule’s law

• Water heater.
• The incandescent bulb (it also generates light).
• Fuse (the fuse melts, burns when the current exceeds a set limit).
• Electric iron.
• Electric stove.
• Thermistors: Thermistors are resistors whose resistance changes when the temperature changes.
• etc.

Examples

Example 1: How much heat does a 2 amp current generate in a wire with a 50 ohm resistor for 2 seconds?

We have: I = 2 amps, R = 5 ohms, t = 2 seconds.

Using the formula: J = I² . R . t , we get: J = (2)² x (5) x (2) = (4) (5) (2) = 40 Joules. Then: 40 Joules of heat are produced.

Example 2: The resistance of an electric bulb is 100 ohms. When 120V is applied across its ends, find the power consumed in 1 hour.

We have. R = 100 ohms, V = 120 volts, t = 1 hour = 3600 s.

Using Ohm’s Law formula, I = V/R. I = 120/100 = 1.2 Amps

Using the formula: J = I² . R . t , we get: J = (1.2)² x (100) x (3600) = (1.44) (100) (3600) = 518 400 Joules. Then he power consumed in 1 hour is 518 400 Joules = 0.144 KWh.

Notes:

• 1 joule = 0.24 calories of thermal energy
• 1 Kilowatt-hour = 1 KWh = 1 000 watt x 3 600 seconds = 3.6 x 10⁶ joules (1 KWh = 3 600 000 joules)