What is a radian?

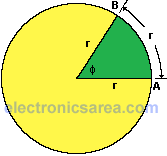
To understand what a radian is, you need to carefully analyze the diagram shown. This diagram shows a circle of radius r. If starting from the point A on the circumference of the circle, we move to a point B, covering exactly the distance r, we will have formed an angle that will be represented as: ø (phi).

Then:

“The radian is the angle that cover the portion of the circumference which is equal
to the length of the radius of the circle”.

The diagram shows a circle of radius r. If we make a full turn. If we start at point A and end at the same point A, we have rotated 360 degrees and as is known, the circumference of a circle is C = 2π r. Passing this value to degrees:

– 2 π r = 360
– ø = 360/2 π
– with π = 3.141592
– ø = 360 / 6.283185
– ø = 57.29578 degrees

In electronics is often better to express the frequency in radians per second (angular frequency)

Angular frequency

The angular frequency is represented by the letter ω (radians per second). The relationship between the frecuency in Hertz and the angular frequency is: ω = 2πf.

where:
– ω = angular frequency
– π = 3.141592 …. (the Pi constant)
– f = frequency in hertz

It is also used to represent the phase angles in radians. Instead of saying 90 degrees out of phase, we say π/2 radians out of phase. 60 degrees out of phase means π/3 radians out of phase.

When we use the symbol π in our calculations, the results of operations are not accurate, because its value is always used rounded. If the π value appears several times, the resulting error is greater. This problem does not exist when we use radians.

In the following video we can see the radian and the number of times that it gets into a circle. Theoretically, in a circle (360 degrees) enters 2π radians which is about 6.28 times a radian.