What is an RC Low Pass Filter?
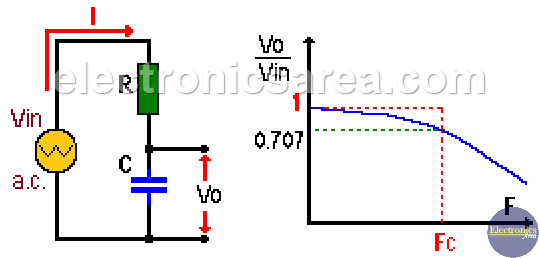
An RC low pass filter is a circuit consisting of a resistor and a capacitor connected in series, as shown in the figure below.
The RC low pass filter allows only frequencies below a certain frequency, called the cutoff frequency (Fc), to pass and eliminates frequencies above that frequency. These RC low pass filters are not perfect, so two analyses are performed.
An analysis with an ideal filter and another with a real filter. The unit of frequency is: Hertz or cycles per second.
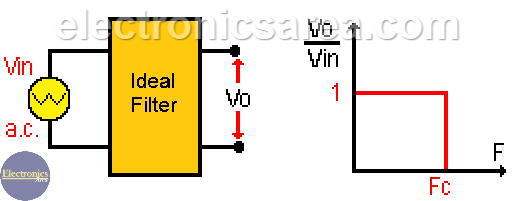
Ideal RC Low Pass Filter
The ideal RC low pass filter is a circuit consisting of a resistor and a capacitor in series, which allows frequencies below the cut-off frequency (Fc) to pass through and eliminates those above it. (see previous figure).
Real RC Low Pass Filter
Capacitive reactance (XC) varies with frequency. At high frequencies (above the cutoff frequency), the capacitive reactance XC is low and the signals of these frequencies are attenuated.
In contrast, at low frequencies (below the cutoff frequency), the capacitive reactance is large, so these frequencies are not affected by the filter.
Using Ohm’s law, we get:
- Vin = I*Z = I*(R2 + XC2)1/2
- Vo = I*XC
- Vo = Vin/(1 + (2πf*RC)2)1/2
where:
- Z = Impedance
- π = Pi = 3.14159
- f = frequency in Hertz
- R = resistance value
- C = capacitor value
The cutoff frequency is the frequency at which the amplitude of the incoming signal drops to 70.7% (0.707) of its maximum value. This occurs when XC = R (capacitive reactance = resistance). When XC = R, the cutoff frequency is Fc = 1/(2*π*R*C).
The band of frequencies below the cutoff frequency (Fc) is called the pass band, and the band of frequencies above the cutoff frequency is called the stop band.
Phase angle of an RC low pass filter
The phase angle of an RC low pass filter as a function of frequency is given by the formula ψ = tan-1 (R / XC).
Note: ( )1/2 = square root.