Millman’s Theorem

Millman’s Theorem states that when there are several voltage sources connected in parallel, each in series with a resistance (internal resistance Ri), the array can be replaced by a single voltage source (VM) in series with an equivalent resistance (RM).

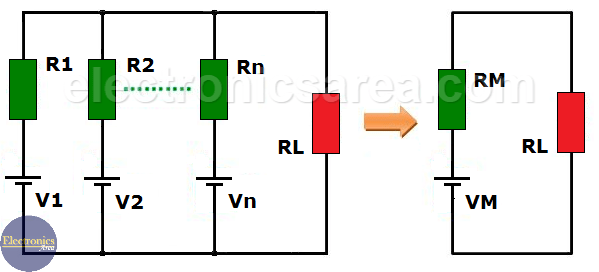
Millman’s equivalent circuit

Many circuits have more than one voltage source, for example: Banks of batteries for emergency lighting, parallel power generators, etc.

Each of these voltage sources, which are in parallel, has a different internal resistance (each source’s own resistance) and the entire set of sources are connected to the load (RL). See diagram of the original circuit (left side of the image).

Millman’s Theorem shows us a simple method to obtain an equivalent circuit (right side of the diagram).

In order to use the Millman’s Theorem, we have to reconstruct the circuit (if possible) into a circuit of parallel branches, consisting of a voltage source and a series resistance (impedance) each or a current source and a parallel resistance (impedance). We’ll use the first option.

How to find the equivalent Millman circuit?

• “RM” is obtained. RM is the value of the equivalent resistance in parallel of all the resistors that are in series with the voltage sources. 1/RM = 1/REq = 1/R₁ + 1/R_{2 +} ….. + 1/R_n.
• VM” is obtained using the following formula:
  VM = (V₁/R₁ + V₂/R₂ + ….. + V_n/R_n) / (1/R₁ + 1/R₂ + 1/R_n).

If there were 3 or more sources with their respective internal resistances, the process would be the same. At the end a circuit is obtained consisting of a voltage source in series with a resistance, which is connected to the load. In our case: RL.

The equivalent voltage source is VM and the equivalent resistor is RM. The diagram shown (right side of the diagram) is the Millman equivalent circuit.

For example

A circuit similar to the previous one with 3 voltage sources, 3 series resistors  and a load resistor.

• V1 = 96V, R1 = 240 ohms
• V2 = 40V, R2 = 200 ohms
• V3 = 80V, R3 = 800 ohms
• RL = 192 ohms

Obtaining RM

1/RM = 1/R₁ + 1/R₂ + 1/R₃  =  1/240 + 1/200 + 1/800  =  0.01417

1/RM = 0.01417, then: RM = 96 ohms.

Obtaining VM

VM = (V1/R1 + V2/R2 + V3/R3) / (1/RM)

VM = 0.4 + 0.2 + 0.1) / (0.01417)  = (0.7) (96) = 67.2 vols. Then VM = 67.2 volts.

RM and VM values ​​found are replaced in the circuit above (see diagram above on the right) to obtain the Millman equivalent circuit for this example.