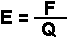The electric Field
When a charge Q is affected by an electrostatic force, there is an electric field. The following formula shows the relation between them.
From the formula, we can see that the unit is: Newton / coulomb (on the MKS system). Newton is the unit of force and Coulomb is the unit of the electric charge.
Note:
– Coulomb = electric charge of 6.28 x 1018 electrons.
– 1 Ampere = 1 coulomb / second
If at some point the electric field is known, we can find the electrostatic force on a charge Q at that point. We can obtain the following by solving the above formula:
Electric Field lines of Force
An electric field can be represented as lines of force (they don’t really exist). They are useful to understand how it works. See the diagram below.
The lines of force show at each point the direction that the electric field (E) has. These lines never intersect with each other, and when they are close it means that the field is more intense.
However, we must take into account that for a given electric field, the number of lines of force is the same. The lines of force always start in the positive charge and end up in the negative charge. See the diagram above.
The Electric Field Unit
The Electric Field Unit could be easily deduced from the following formula: E = F/Q.
The electric field is the quotient of an electrostatic force F and of an electric charge Q. It has the unit of Newton / Coulomb. To obtain the unit of electric field, we can use other values, which can help us to make the electric field concept clearer.
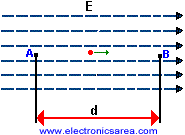
An F force will be applied on a charge that is placed on an electric field E. Now, if this charge is moved from point A to point B on the opposite direction of the force, an amount of work (W) will be done. This work is defined as: W = F x d = Q x E x d
F = Q x E (clearing up F from the formula that appears at the top). From the last formula, we obtain: W/Q = Exd.
Electric Field Unite
The E x d expression is called potential difference between the points A and B, and it is represented as VAB. Then VAB = E x d. Solving the last equation to the electric field (E) we obtain: E = VAB/d and the unit is: volts/meter.