Air core inductor inductance calculation
There are some occasions when we have an air core inductor, and we don’t know what its value is. There is an easy way to obtain the air core inductor inductance if you have the external measurements of this component.
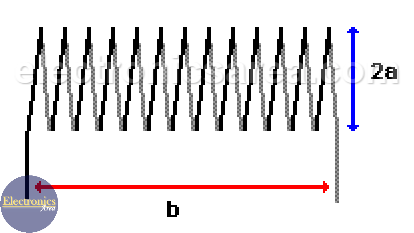
You can use the following formula: L(µH)= (0,393 a2N2)/(9a+10b), where:
- n: is the number of spires
- a: is the radius in centimeters
- b: is the length in centimeters.
This formula is a good approximation of the inductance for a length equal or greater to 0.8a (0.8 times the inductor radius).
Examples of air core inductor calculations
Example # 1:
If we have an inductor with 32 spires, 13 turns per centimeter and a diameter of 25 mm. What the inductance will be?
Using the formula: L(µH)= (0,393 a2N2)/(9a+10b) with the following values:
- a = 25 mm/ 2 = 2.5 cm/ 2 = 1.25 centimeters
- b = 32 / 13 = 2.46 cm
- n = 32 turns
Then: L = (0,393 x (1.25)2 x 322) / (9 x 1.25 + 10 x 2.46) = 17.54 µHenries (µH)
Example # 2:
We want to build a 10 µH inductor, with 2.54 centimeters in diameter and a length of 3,175 centimeters. Then:
- a = 2.54 centimeter / 2 = 1.27 centimeters
- b = 3,175 centimeters
- L = 10 µHenries (µH)
We clear from the original equation the n variable: n = [10 x (9a+10b) / (0,393 x a2)]1/2 , and by replacing the values we get the following:
n = [10 x (11.43 + 31.75) / 0,393 x 1,613]1/2 = 680 1/2 = 26.1 spires
Notes:
- the parentheses to the 1/2 power is the same as a square root
- µHenry = microhenry = µH
