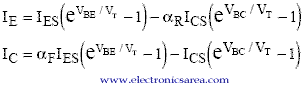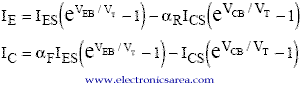Home / Semiconductors /
The Bipolar Transistor (Ebers Moll Model)
The bipolar transistor is an electronic device that originates a big evolution in the electronics field. The basic features of the bipolar transistor are introduced on this topic. We’ll study the basic model (Ebers Moll Model) of these devices and their use in the analysis of circuits biasing.
Biasing a bipolar transistor is necessary for many linear and non-linear applications, because it establishes the voltage ranges and the direct current that is going to circulate on the transistor.
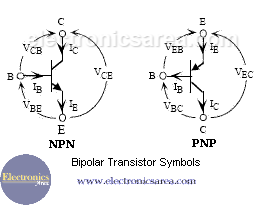
A bipolar transistor has two back to back PN junctions. Physically, the transistor consists of three regions: emitter, base and collector. The base region is very thin (<1 µ m).
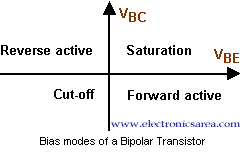
When the transistor operates in active mode, The emitter-base junction is forward biased and the base-collector junction is reverse biased. In this case, the directions of the currents and the voltages are shown in the above pictures.
The relation between the currents is: IE = IB + IC, and …
VCE = VCB + VBE for an NPN transistor.
VCE = VEB + VBC for an PNP transistor.
Ebers Moll Model equations of a Transistor
Ebers and Moll created a model between the current and voltages in the transistor terminals . This model, known as the Ebers Moll model sets the following general equations, for an NPN transistor:
IES and ICS represent saturation current for emitter and collector junctions, respectively. αaF is the common base forward short circuit current gain (0.98 to 0.998) αR is the injection of minority carriers fraction. In a PNP bipolar transistor, the Ebers Moll model equations are:
For the ideal transistor, the previous four parameters are related by the Reciprocity Theorem. αFIES = αRICS. Typical values of these parameters are: αF = 0.99, αR= 0.66, IES = 10-15A, ICS = 10-15A.
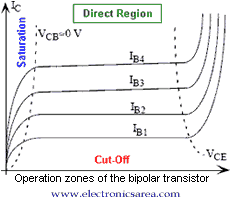
Operation Zones of a Bipolar transistor