What is an Alternating Current?

Dec 112019

The alternating current (AC)

The difference between an alternating current and a direct current is that a direct current only flows in one direction. Alternating current circulates in one direction, then the opposite direction, and repeats this process continuously.

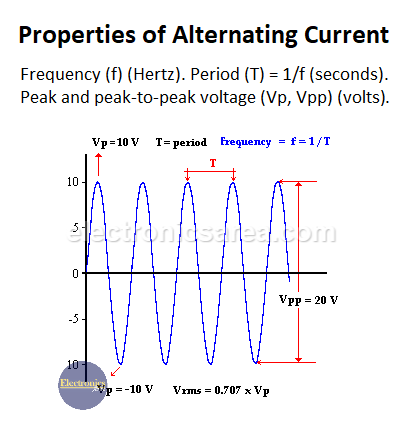
This is the type of electric current that powers the appliances in our homes, such as TVs, stereos, washing machines, and refrigerators. The following picture shows the magnitude variation of an alternating voltage. It first goes up, then down, forming a sine wave. It behaves the same way as the current.

This voltage and current vary continuously, and we can use the formula V = V_p x sin(Θ) to determine the voltage at a specific time. V = V_p x sin(Θ) to determine the voltage at a specific time. Note: θ = wt = 2πft, where:

π = 3.1416
f = frequency
t = time

Vp is the maximum value of the wave, and θ is the angular distance measured in degrees. See the diagram.

Looking at the last picture, we see a periodic sine wave, which repeats continuously. A complete cycle of this sine wave is 360 degrees. Using the above formula, we can find the voltage magnitude at any time.

For each angular distance θ, there is a different voltage. In some cases, the voltage is positive, and in others, it is negative when the polarity reverses.

Properties of Alternating Current

Frequency (f): The number of cycles that a signal (voltage or current) completes in one second. The unit of frequency is: Hertz
Period (T): The time it takes for a signal to repeat. The period has the following formula: T = 1/f, meaning the period (T) is the inverse of the frequency (f).
Peak-to-peak alternating current voltage (Vpp)
Looking at the picture, we see that there is a maximum and minimum voltage.

The difference between these two alternating current voltage values is called the peak-to-peak voltage (Vpp)), which is twice the peak voltage (Vp). See the picture below for reference.

RMS value: RMS Voltage (Vrms) You can calculate the RMS value of an alternating current voltage using the following formula: Vrms = 0.707 x Vp. This is the voltage value obtained from a VOM/multimeter.

Now, here’s something to think about:

When we use a VOM to test the AC voltage in our homes, we find that it will be around 110 or 220 volts, depending on the country. This is an RMS voltage.

What are the peak voltage (Vp) and peak-to-peak voltage (Vpp) of this signal?

Using the formula above: Vp = V(rms)/0.707 and V(pp) = 2V_p.

Case 1: Vrms = 110 V;