Mesh Current Method in a Resistor Network

Mesh current method in a resistor network

The mesh current method is very useful to know all the current in a network of only resistors. This method, a little more extended, is also applied to circuits where there are resistances and reactances.

Using the mesh current method, resistors current values are calculated, then it is easy to obtain their voltages and their consumed power.  This method is based on Kirchhoff’s voltage Law.

The Mesh-Current Method or Loop Current Method is a technique used to find the currents circulating around a mesh with in any closed path of a circuit.

Steps to follow to make analysis by the mesh current method:

1. Draw the circuit to be analyzed so that there is no one connection crossing over another. (if possible)
2. Convert current sources into voltage sources.
3. Draw the direction of the currents in the sense of the needles of the clock. The currents are called I1, I2, I3, … .etc. See example at the end.
4. Make a table with the equations obtained from the circuit (Kirchhoff’s law of voltages). The number of rows in the table is the same as the number of currents established in step 3.
5. Columns with unknown variables are placed on the left side of the equal sign, and the column with the constant values on the right side.

You may also want to read the Nodal analysis method

Example of Mesh Current Method in a Resistor Network

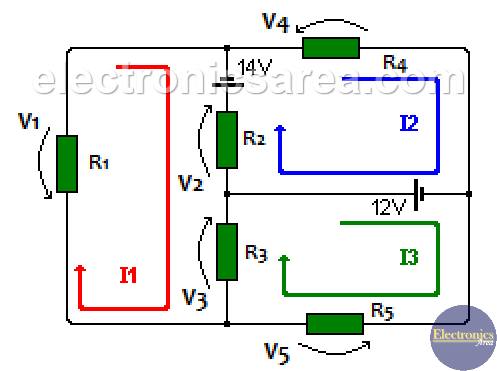
Analyze the following circuit:

For the I1 mesh: V1 + V2 + V3 – 14V = 0    (1)
For the I2 mesh: -V2 + 14V + V4 – 12V = 0    (2)
For the I3 mesh: -V3 -12V + V5 = 0   (3)

Voltages in each resistor are:

V1 = I1 x R1
V2 = (I1-I2) x R2
V3 = (I1-I3) x R3
V4 = I2 x R4
V5 = I3 x R5

We replace the previous voltage values in formulas (1), (2) and (3), and we obtain:

For the I1 mesh: I1 x R1 + (I1-I2) x R2 + (I1-I3) x R3 – 14V = 0
For the I2 mesh: – (I1-I2) x R2 + 14V + I2 x R4 – 12V = 0
For the I3 mesh: – (I1-I3) x R3 -12V + I3 x R5 = 0

We use the following values of the resistors:

R1 = 10 ohms, R2 = 6 ohms, R3 = 4 ohms, R4 = 8 ohms, R5 = 2 ohms.

For the I1 mesh: 10I1 + 6 (I1-I2) + 4 (I1-I3) – 14V = 0
For the I2 mesh: -6 (I1-I2) + 14V + 8I2 – 12V = 0
For the I3 mesh: -4 (I1-I3) – 12V + 2I3 = 0

Then we get:

For the I1 mesh: (10 + 6 + 4) I₁ – 6I₂ – 4I₃ -14V = 0 ….  20I₁ – 6I₂ – 4I₃ = 14
For the I2 mesh: 6I₂ + 8I₂ – 6I₁ + 14V – 12V = 0  ….   6I₂ + 8I₂ – 6I₁ = -2
For the I₃ mesh: 4I₃ + 2I₃ – 4I₁ = -12

The final equations are: (as indicated in step 4

20I₁ – 6I₂ – 4I₃ = 14
– 6I₁ + 14I₂ + 0I₃ = -2
– 4I₁ + 0I₂  + 6I₃ = -12

Since there are three unknowns values (I1, I2, I3), there are three rows in the table. Using the substitution method or the determinant’s method, the following values are obtained:

I1 = 0.348 amps
I2 = 0.006285 amps
I3 = -1.768 amps. The minus sign indicates that the direction of current I3 is opposite to that assumed at the beginning.