What does the Maximum Power Transfer Theorem say?
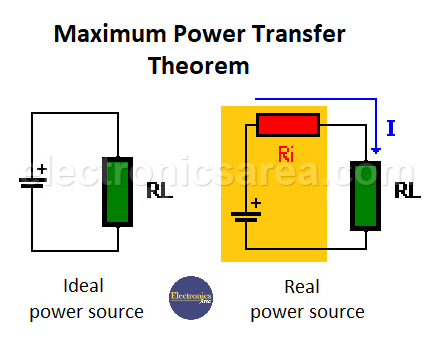
“The maximum power transfer to the load is obtained when the load resistance RL is equal to the internal resistance of the source Ri”.
But why is that the case?
Real voltage sources have the equivalent circuit shown in the figure below, where V = I x Ri + VL.
- If the value of Ri (internal resistance in power supplies) is high, only a small part of the voltage will appear in the load due to the drop in the internal resistance of the source.
- If the drop in the internal resistance Ri is small (the case of the new voltage source with a small Ri), almost all the voltage will appear at the load.
Proof of the Maximum Power Transfer Theorem
If in the circuit Ri = 8 ohms, RL = 8 ohms, and V = 24 volts, then I = V / (Ri + RL) = 24 / 16 = 1.5 amps. This means that the voltage across RL is VRL = I x R = 1.5 x 8 = 12 volts.
This data tells us that when the internal resistance Ri and RL are equal, only half of the original voltage appears in the load (RL). The power in RL will be P = I2 x RL = 1.52 x 8 = 18 watts (watts), which means that the same power is lost in the internal resistance.
Internal resistance of a power source
If we now increase or decrease the value of the load resistance and perform the same calculations as before to find out the power delivered to the load, we can see that it is always less than the 18 watts obtained when RL = Ri (remember that Ri is always equal to 8 ohms).
For example:
If RL = 4 ohms
I = V / (Ri + RL) = 24 / 12 = 2 amps, then
P = I2 x RL = 22 x 4 = 16 watts
The power obtained is less than 18 watts.
If RL = 12 ohms
I = V / (Ri + RL) = 24 / 20 = 1.2 amps
P = I2 x RL = 1.22 x 12 = 17.28 watts
The power obtained is less than 18 watts.
As you can see, the power delivered to the load is always less than 18 watts, so for maximum power transfer, the load resistance must match the internal resistance in the power sources.
Maximum Power Transfer Theorem with AC Power Sources
In the case of AC power sources, maximum power transfer is achieved only when the value of the load impedance is equal to the complex conjugate of the source impedance. (Their resistances must be equal, and their reactances must be equal in magnitude but opposite in sign).