The Decibel
The decibel expresses a ratio of quantities, not a quantity itself. It does not express an exact amount. The decibel expresses how many times more or less a quantity is relative to another quantity. It is an expression that is not linear but logarithmic. It is a relative unit of measurement.
At audio frequencies, a change of 1 decibel (dB) is barely noticeable. The decibel is abbreviated to dB. There is also the Bel. 1 Bel = 10 dB.
Voltage Gain (Δv) in Decibels
The voltage gain is obtained by dividing the output voltage by the input voltage in an amplifier. Δv = Vout / Vin.
For example: If an amplifier has an input signal of 0.1 Vpp (peak-to-peak volts) and an output signal of 10 Vpp, the voltage gain is: Δv = 10 / 0.1 = 100.
Voltage ratio expressed in dB
If you have two voltages V1 and V2, the ratio V2/V1 in dB is: dB = 20 log10 (V2/V1)
Voltage gain in dB = 20 log10 (10/0.1) = 40 dB
Power Gain (Δp) in Decibels
The power gain is obtained by dividing the power delivered at the output terminals by the power received at the input terminals in an amplifier. Δp = Pout / Pin
For example: If the input power of the amplifier is 0.1 uW (microwatt) and the output power is 5 mW (miliwatt). The power gain is: Δp = 5 mW / 0.1 uW = 5000 uW / 0.1 uW = 50 000.
Power ratio expressed in dB
If there are two powers P1 and P2, the ratio P2/P1 in dB is: dB = 10 log10 (P2/P1)
dB = 10 log10 (5000/0.1) = 46.99 dB
Negative amplification
For example: An amplifier with:
- V1 = input voltage = 100mV
- V2 = output voltage = 70.7mV
The amplification is the ratio between the output voltage V2 and the input voltage V1.
dB = 20 log10 (70.7/100)
dB = 20 log10 (0.707)
dB = 20 x (-0.1506)
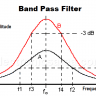
dB = -3.012 dB
That means that there is a negative amplification.
Why use the decibel system?
The reason is very simple. When we have a system with gains and losses (negative gains). It is much easier to add or subtract the gains (not multiply them) to get the final gain.
voltage-current-power-gain-amplifier