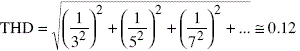Sinusoidal Oscillators

Sinusoidal oscillators play an important role in electronic systems that use harmonic signals. Despite that, in many instances are known as linear oscillators, it is necessary to use some non-linear feature to generate a sine wave output.

In fact, the sinusoidal oscillators are essentially non-linear which complicates the technical design and analysis of such circuits.

The design of oscillators is done in two phases: a linear method based in the frequency domain using the analysis of feedbacked circuits, and a non-linear method, using nonlinear mechanisms for the control of the amplitude.

An oscillator is basically an autonomous circuit. In other words, this circuit is capable of generating a periodic sinusoidal signal with no need for any input.

A fundamental difference with multivibrator circuits is that these are not linear circuits (based on comparators, Schmitt triggers, …) as opposed to the quasi-linear circuits of the oscillators

The quality of the sine wave is expressed through the total harmonic distortion coefficient or THD, defined as:

Where Dk represents the relationship between the amplitude of the harmonic k and the fundamental harmonic described in Fourier series.

For example, the Fourier transform of a triangular wave has only odd harmonics, whose amplitude on the fundamental harmonic is 1/k. In this case, the TDH takes the value:

In other words, a triangular wave is a rough approximation of a sine wave with a THD of 12%. It is clear that the purpose of the sinusoidal oscillators is to generate signals with THD = 0.