BCD Code
In order to share information, which is in digital format, it is common to use binary and hexadecimal representations. There are other methods of representing information and one of them is the BCD code or Binary coded decimal.
With this code, it is easier to see the relationship between a decimal number (base 10) and the corresponding number in binary (base 2)
This code uses 4 binary digits to represent a decimal digit (0 to 9) (see in the two examples that follow), however when converting from a binary number to another decimal, there is no direct relationship between the binary number and the decimal number.
There are other codes, like the Gray code where there is special ordering of binary numbers, so two successive values differ only in one bit. It is used for position detectors where you need to figure out relative position.
Decimal to BCD code conversion examples
Example 1: The direct conversion of the decimal number 85 to binary is: 8510 = 10101012.
The representation of the same decimal number in BCD is shown in the following image.
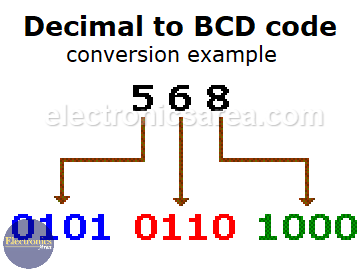
Example 2: The direct conversion of the decimal number 568 to binary is: 56810 = 10001110002.
The representation of the same decimal number in BCD is shown in the following image.
As you can see, from the two previous examples, the representation of the binary number does not resemble the final BCD representation.
How to get the BCD code of each decimal number?
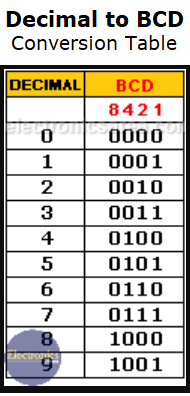
In order to obtain the BCD equivalent of each decimal digit from the previous numbers, a “weight” or “value” is assigned according to the position the digit occupies.
This “weight” or “value” follows the following order: 8 – 4 – 2 – 1. (It is a weighted code). The last example shows that the number 5 is represented as: 0 1 0 1.
- The first “0” corresponds to 8,
- the first “1” corresponds to 4,
- the second “0” corresponds to 2,
- the second “1” corresponds to 1.
From the chart above: 0x8 + 1×4 + 0x2 + 1×1 = 5
The BCD code that has the “weights” or “values” described above is called: Natural BCD code. This code counts as a normal binary number from 0 to 9, but numbers from ten (1010) to fifteen (1111) are not allowed because, for these numbers, there is no equivalent to a decimal number.
Applications
This code is used, among other applications, to represent decimal numbers on 7 segment displays.
Notes: The subscript 2 and 10, are used to represent, in the first case, a binary number and in the second case a decimal number.